Arbitrary Computation on Infinite Chessboards

Recently, I watched a YouTube video by Wrath of Math, entitled “Why You Can’t Bring Checkerboards to Math Exams”. In this short, Wrath of Math demonstrates a binary multiplication and division algorithm for 8-bit integers. This algorithm is just one example of computations on unconventional items. While multiplication and division are interesting as they are, one may ask what the natural limits of computation are on a chessboard. Can one compute anything on a chessboard? For the infinite case, the answer may not be what you expect.

Languages and the Limit of the 8x8 Chessboard

When viewing the chessboard at face value, it is not immediately clear what can be computed on it. In the standard game of chess, we only have finite types of pieces (six black and six white pieces), and only 64 squares to place them on. While the usual interpretation of computations is via the route of algorithms, as in a set of steps to achieve solutions to problems, there are no definitive ways to construct standardized algorithms on the chessboard. To contextualize the chessboard more abstractly, we introduce the concept of languages:

Definition 1: An alphabet is a finite set of charecters $\Sigma$.

Definition 2: A language is a set of finite-length strings from an alphabet $\Sigma$. That is: $L \subseteq \Sigma^*$

In layman’s terms, a language is simply a set of strings. As an example, a hypothetical language on ${0,1}$ could be:

\[L = \{0, 1, 01, 10101, 1011, 11111\}\]

Languages, while unassuming and straightforward at first, actually possess one ability that makes them incredibly useful for contextualizing computation: we can use them to encode problems.

If we had a problem $P$ and a set of valid solutions $x_1,x_2,…,x_n$, as long as we can encode these solutions (by a function $e$) as a set of strings over some alphabet $\Sigma$, ${e(x_1), e(x_2), …, e(x_n)}$ would be a valid language. Specifically, this language encodes the “yes” solutions to $P$. This leads us to a direct way to consider the limits of computations on $P$: find what kinds of languages can and can not be encoded onto a chessboard.

To do so, we denote $C$ to be the set of possible placements of an arbitrary number of chess pieces on a chessboard, regardless of the typical rules of chess. The size of this set is a whopping $13^{64}$: each square can have one of six white or black pieces, or none, on all 64 squares. We define the transition function $\delta: C \rightarrow C$ to be the set of possible moves from any one state to any other. It is worth noting that the term “transition function” is somewhat of a misnomer. Typically, there are many possible moves from any state to any other, making this a relation by technicality. For now, we will disregard exactly which moves are considered legal, as it does not alter the theoretical limits of language recognition on our chessboard. We now will proceed to show that $C$ can not possibly be Turing-complete (and thus can not compute anything):

Since the number of states $C$ that can be recognized is $13^{64}$, this implies that any sequence of moves can only take on finitely many unique states, albeit a truly massive amount. By the pigeonhole principle, if our computation path is longer than $13^{64}$ moves, we must revisit some state more than once.

This dependency on cyclical structure after a finite number of computational moves disallows the chessboard from computing arbitrarily without repetitions. In computer science terms, the chessboard behaves equivalently to a finite state machine. This means that, at most, the chessboard can recognize a subset of the regular languages. If a computation requires an infinite number of steps not bounded by a single cycle, the chessboard will be unable to recognize it. Such a language could be $L = {a^n b^m \mid n = m + 3}$, where no single pre-determined cycle can account for the interdependence of the powers of $a$ and $b$.

The logic of our argument mirrors the Pumping Lemma; a famous theorem that provides a bound on what’s possible to recognize on a finite state machine. In fact, no finite chessboard will suffice here, as while the state space $C$ can grow arbitrarily large, it is never infinite, meaning we can always find arbitrarily long computation paths that force repetitions in the way that we did with the 8x8 chessboard.

So let’s pump the gas a little and move to the infinite chessboard!

the Infinite Chessboard and the Turing Machine

We now move to the case where our chessboard is not 8x8, but infinite in both the horizontal and vertical directions, extending from row 0. Each possible arrangement of pieces now represents one of countably many configurations, escaping the confines of language recognition on finite-sized chessboards.

With this in mind, we can begin to construct a method of computation similar to that of the Turing Machine on our chessboard. To better understand how, let us first visit the formal definition of a Turing Machine:

Definition 3: A Turing Machine is a tuple $M = \langle Q, \Gamma, b, \Sigma, \delta, q_0, F \rangle$ where:

1. $\Gamma$ is a finite, non-empty set of symbols used as an alphabet on the tape;
2. $b \in \Gamma$ is the blank symbol (the only symbol allowed to occur on the tape infinitely often and is the default symbol on the tape.)
3. $\Sigma \subseteq \Gamma \setminus { b }$ is the set of tape symbols that can appear on the tape initially (at time 0);
4. $Q$ is a finite, non-empty set of states the machine can be in;
5. $q_0 \in Q$ is the starting state of the turing machine;
6. $F \subseteq Q$ is the set of accepting states;
7. $\delta : (Q \setminus F) \times \Gamma \to Q \times \Gamma \times {L, R}$ is a partial function, where $L$ and $R$ denote left and right shifts respectively.

While it may seem unintuitive at first, we are simply defining a set of transitions $\delta$ defining the movements of a “head” over an infinite tape. The tape is initialized with an input string over $\Sigma$ and is set to the state $q_0$. An input string over $\delta$ specifies, based on the current state and symbol on the tape, a new state for the machine to be in, a symbol to overwrite the current state with, and whether to move the head left or right.

The machine then follows the deterministic set of moves laid out by $\delta$, and if the machine ends on an accepting state $F$ in finite time, the string is accepted. We define the language $L(M)$ defined by the Turing Machine M to be the set of input strings that the Turing Machine accepts. If the Turing machine ends on a state not in $F$ and has no defined moves left, the machine halts, and that particular input string is rejected.

To construct our new model of computation, we take heavy inspiration from the original Turing Machine. Our goal is to build a set of moves on the chessboard that effectively mimics the movements of the Turing Machine.

It should be noted here that our initial alphabet and tape alphabet $\Sigma$ and $\Gamma$ will both be ${0, 1}$. We define 0 to be the presence of a pawn on a given square and 1 to be the lack of a pawn on a square. We then define our input string and tape, placing them on row 4. The string input exists on all columns before e, and the write tape exists on all columns after e. Nothing exists on row e, except for the starting position of our “head”, which will be the knight on e2. For the sake of brevity, we refer to row 4 as the “memory row.”

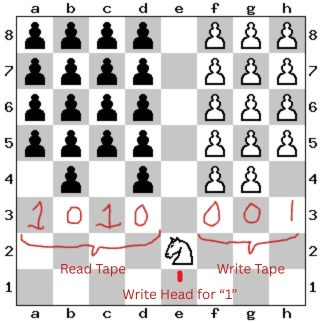
The head can make 3-move sequences to move exactly one square to the left or right, positioning it to read and write for arbitrary squares on the memory row:

Let $M_{d\rightarrow c}$ denote the movement of the head from column d to c on row two, respectively. With the movement of the head defined, we can now define the process of reading and writing on our chess-based Turing Machine.

Since we have exhausted the purpose of movements in defining the head, the only action left to work with is the act of capturing. Thus, we define a “read” by the knight to be an attempted capture on a square on the memory row. If the capture is successful, the machine reads a 0, since a pawn on a square denotes a 0; if the capture is unsuccessful, the knight reads a 1. After an attempted read, the knight will always make one move back to its starting position. We will denote a read on cell $\alpha$ on memory row as $I_\alpha$. If a knight reads a 0, the piece will be destroyed, leaving a 1 in its place. Thus, to preserve the information on the tape, after the knight returns to its starting position, all the pawns in the succeeding rows must move down exactly one square to reset the machine.

To write a 1 on column $\beta$, the knight captures on that square, just like a read, denoted $O_\beta 0$. But to write a 0, all the pawns on a given column need to move down exactly one square to write a 1. We denote the (infinite) set of moves to write a 1 on column $\beta$ to be $O_\beta 1$. Thus, the task of writing is divided into two different structures, unlike the typical Turing machine.

The last thing to consider is the act of halting. We construct an accepting state as one where the knight returns to a row with an index less than 1 on column e. We can naturally act this out on the chessboard by artificially restricting it to where there are no valid outgoing moves for the knight once it enters row 0. Then, if the knight captures any pawn after row 4, we define it to be a rejecting halt, and again define there to be no valid moves for the knight after this point.

With the standard operations of the Turing Machine defined on a chessboard, we have been able to create a (highly impractical) model of arbitrary computation. Every possible move a Turing machine can make can be emulated one-to-one on our infinite chessboard.

Conclusions

This exercise demonstrates that while the Turing Machine itself may seem abstract and byzantine, it can be emulated readily in a myriad of different ways, even on a chessboard. While impractical in itself, it creates an interesting dichotomy:

• The finite chessboard behaves like a finite state machine, limited to recognizing only regular languages due to its finite number of configurations.
• The infinite chessboard behaves more like a turing machine, able to conduct arbitrary computation.

We have also demonstrated that computation in the theoretical sense need not be limited to digital electronics, and many non-digital systems can effectively emulate the act of computation. In a way, this demonstrates the beauty of computation: that endowed structure in itself can create universal machines.

---